Fractals: A Hidden Infinity
Beautiful, damn hard, increasingly useful. That's fractals.
~ Benoit Mandelbrot
Even in the midst of chaos, there appears to be some semblance of order. In 1975, French and American mathematician Benoit B. Mandelbrot made sense of this apparent contradiction by consolidating hundreds of years of previous research into the concept of fractals. Fractals are geometric shapes that have the same, or at least similar, repeating structure at different scales of magnification, so that each component represents a miniature copy of the whole. In theory, this condition of self-similarity will yield an infinite pattern via the process of recursion, which involves the application of a simple set of rules over and over again to produce the same effect or structure.
Interestingly, there are countless examples of fractals in the natural world. Many biological structures, from ferns to animal color patterns, can be rendered in mathematical notation as a result of being fractals. Visually, of course, biological fractals can be discerned due to advancements in imaging techniques, such as those associated with the microscope.
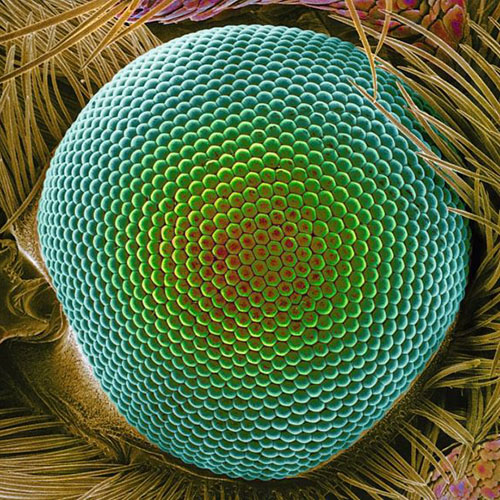
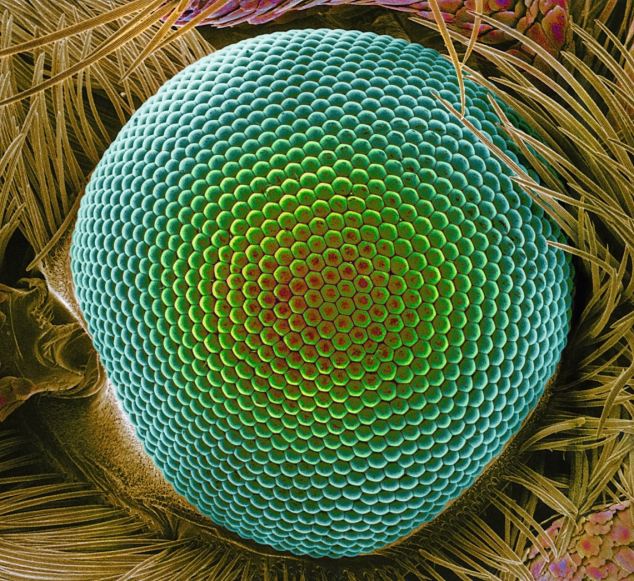
“Up close: The diamondback moth's eye.” Photo by Daniel Scharf.
Copyright © by David Scharf, 1977, 2005.
www.scharfphoto.com

